Модель прогнозирования ARIMAX: скользящее среднее.

Модели случайных процессов, имеющих место в системах передачи информации, зачастую могут быть представлены в виде временных рядов. В частности частотно-селективные и временные селективные замирания могут быть представлены посредством моделей авторегрессии. При этом повышение порядка модели позволяет повысить степень ее адекватности реальному случайному процессу. В лабораторной работе рассмотрены два типа временных рядов - авторегрессионные последовательности и процессы со скользящим средним.

Цель работы: изучение авторегрессионных моделей, а также моделей скользящего среднего, позволяющих имитировать случайные процессы с заданным спектром и корреляционной функцией; анализ статистических характеристик имитируемых случайных процессов.

где - независимые отсчеты гауссовой случайной величины с нулевым средним и единичной дисперсией, .

Автокорреляционная функция:

Нормированная автокорреляционная функция: , .

Дисперсия: , где - дисперсия белого шума.

Автокорреляционная функция:

Дисперсия: .

Спектр:

3. Модель скользящего среднего первого порядка

где - независимые гауссовы случайные величины, .

Автокорреляционная функция: , .

Дисперсия: .

Спектр: , .

4. Модель скользящего среднего второго порядка

Автокорреляционная функция:

Дисперсия: .

Спектр:

Порядок выполнения работы:

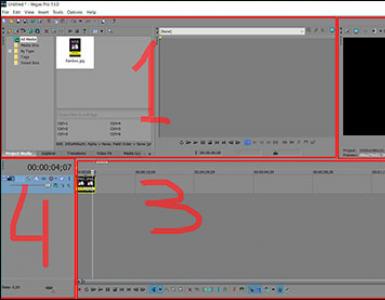
1. Загрузить пакет SciLab_4_1 и выбрать опцию Editor. Перенести соответствующие Script-файлы в программное окно.

2. Получить графики временных реализаций (Time Realization), корреляционных функций (Correlation Function) и спектров (Spectrum) для соответствующих моделей временных рядов: авторегрессии 1-го порядка (AR_1), авторегрессии 2-го порядка (AR_2), скользящего среднего 1-го порядка (МА_1), скользящего среднего 2-го порядка (МА_2) в соответствии с вариантом задания (таблица 1). При этом в программном окне коэффициентам авторегрессионного уравнения и соответствуют обозначения G1 и G2; коэффициентам корреляции и уравнений авторегрессии соответствуют обозначения p 1 и p 2; коэффициентам и уравнений скользящего среднего - обозначения J 1 и J 2, соответственно. В отчете должно быть представлено 12 графиков.

• 3. Вычислить дисперсию случайного процесса для каждой модели временного ряда (значение в окне Variance в режиме Time Realization - VarZ).
• 4. Вычислить значения и для модели авторегрессии второго порядка.

5. Вычислить значения и для моделей скользящего среднего.

Таблица 1. Варианты заданий

• 1. Название работы, ФИО студентов, цель работы.
• 2. Необходимые теоретические сведения.
• 3. Графики временных реализаций, корреляционных функций и спектров для соответствующих моделей временных рядов: авторегрессии 1-го и 2-го порядка, скользящего среднего 1-го и 2-го порядка.
• 4. Вычисленные значения дисперсии, а также соответствующих коэффициентов корреляции.
• 5. Выводы по работе.

Контрольные вопросы:

Откуда произошло название «скользящее среднее»?

Дайте определение понятия «корреляция».

Что характеризует корреляционная функция случайного процесса?

Что характеризует спектр сигнала?

Как вычислить энергию сигнала, зная спектральную плотность мощности?

Существуют ли неустойчивые процессы со скользящим средним?

Каково условие стационарности для процесса авторегрессии 2-го порядка?

Как влияет изменение знака перед коэффициентом на форму спектра процесса авторегрессии 1-го порядка?

Можно ли назвать процесс со скользящим средним коррелированным?

Script-файлы:

Коэффициенты G1 и G2 нужно вычислить самостоятельно по формулам, исходя из заданных (в варианте задания) нормированных коэффициентов корреляции p1 и p2 .

q=grand(1,N,"nor",0,1)

p=0.9; z(1)=grand(1,1,"nor",0,1);

z(i)=p*z(i-1)+q(i);

S=2./(1+p^2-2*p*cos(2*3.1415926*w));

G1=0.75; G2=-0.5;

q=grand(1,N,"nor",0,1);

z(1)=grand(1,1,"nor",0,1); z(2)=grand(1,1,"nor",0,1);

z(i)=G1*z(i-1)+G2*z(i-2)+q(i);

G1=0.75; G2=-0.5; p(1)=G1./(1-G2); p(2)=G1*p(1)+G2;

p(i)=G1*p(i-1)+G2*p(i-2);

set("figure_style","new")

a=get("current_axes");

a.data_bounds=;

G1=0.75; G2=-0.5;

varZ=(1./((1-G2).^2-(G1)^2)).*((1-G2)/(1+G2));

S=2./(1+(G1)^2+(G2)^2-2*G1.*(1-G2).*cos(2*3.1415926*w)-2*G2*cos(4*3.1415926*w));

J=0.5; q=grand(1,N,"nor",0,1);

z(i)=q(i+1)-J*q(i);

S=2./(1+J^2-2*J*cos(2*3.1415926*w));

J1=0.7; J2=-0.3; q=grand(1,N,"nor",0,1);

z(i)=q(i+2)-J1*q(i+1)-J2*q(i);

J1=-0.7; J2=-0.7;

varZ=(1+J1^2+J2^2);

S=2.*(1+(J1)^2+(J2)^2-2*J1.*(1-J2).*cos(2*3.1415926*w)-2*J2*cos(4*3.1415926*w));

Библиографический список

• 1. Бокс, Дж. Анализ временных рядов. Прогноз и управление. В 2 вып. Вып. 1 / Дж. Бокс, Г. Дженкинс; пер. с англ. А. Л. Левшина, под ред. В. Ф. Писаренко. - М. : Мир, 1974. - 406 с.
• 2. Васильев, К. К. Методы обработки сигналов: учебное пособие / К. К. Васильев. - Ульяновск: УлГТУ, 2001. - 80 с. (имеется электронная версия)
• 3. Васильев, К.К. Математическое моделирование систем связи: учебное пособие / К. К. Васильев, М. Н. Служивый. - Ульяновск: УлГТУ, 2008. - 168 с.

где последовательность случайных величин d1, d2,… образует белый шум.

Условия стационарности процесса, генерируемого моделью (2.23), также формулируются в терминах корней его характеристического уравнения

1 - a1z - a2z2 -…- apzp = 0.

Для стационарности процесса необходимо и достаточно, чтобы все корни характеристического уравнения лежали бы вне единичного круга, т.е. превосходили бы по модулю единицу.

Автокорреляционная функция процесса (2.23) может быть вычислена с помощью рекуррентного соотношения по первым p ее значениям r(1),…, r(p). Это соотношение имеет вид:

r (t) = a1r(t - 1) + a2r(t - 2) +…+ apr(t - p), t = p + 1, p + 2, . (2.24)

Частная автокорреляционная функция процесса (2.23) будет иметь ненулевые значения лишь при t £ p; все значения rчаст(p) при t > p будут нулевыми. Это свойство частной автокорреляционной функции AR(p)-процесса используется, в частности, при подборе порядка в модели авторегрессии для конкретных анализируемых временных рядов. Если, например, все частные коэффициенты автокорреляции, начиная с порядка k, статистически незначимо отличаются от нуля, то порядок модели авторегрессии естественно определить равным p = k - 1.

Идентификация модели авторегрессии p-го порядка основана на соотношениях, связывающих между собой неизвестные параметры модели и автокорреляции исследуемого временного ряда. Для вывода этих соотношений последовательно подставляются в (2.24) значения t = 1, 2,…, p. Получается система линейных уравнений относительно a1, a2,…, ap:

(2.25)

называемая уравнениями Юла–Уокера. Оценки для параметров ak получим, заменив теоретические значения автокорреляций r(k) их оценками и решив полученную таким образом систему уравнений.

Оценка параметра получается из соотношения

заменой всех участвующих в правой части величин их оценками.

2.3.2. Модели скользящего среднего порядка q (МА(q)-модели)

Рассмотрим частный случай общего линейного процесса (2.13), когда только первые q из весовых коэффициентов bj ненулевые. В это случае процесс имеет вид

et = dt - q1dt-1 - q2dt-2 -…- qqdt-q, (2.26)

где символы -q1,…, qq используются для обозначения конечного набора параметров b, участвующих в (2.13). Процесс (2.26) называется моделью скользящего среднего порядка q (МА(q)).

Двойственность в представлении AR - и МА-моделей и понятие обратимости МА-модели. Из (2.13) и (2.14) видно, что один и тот же общий линейный процесс может быть представлен либо в виде AR-модели бесконечного порядка, либо в виде МА-модели бесконечного порядка.

Соотношение (2.26) может быть переписано в виде

dt =et + q1dt-1 + q2dt-2 +…+ qqdt-q.

dt = et - p1et-1 - p2et-2 -…, (2.27)

где коэффициенты pj (j = 1, 2,…) определенным образом выражаются через параметры q1,…, qq. Соотношение (2.27) может быть записано в виде модели авторегрессии бесконечного порядка (т.е. в виде обращенного разложения)

Известно (см., например, [Бокс, Дженкинс, (1974)]), что условие обратимости МА(q)-модели (т.е. условие сходимости ряда ) формулируется в терминах характеристического уравнения модели (2.26) следующим образом:

Все корни характеристического уравнения должны лежать вне единичного круга, т.е. |zj| > 1 для всех j = 1, 2,…, q.

Основные характеристики процесса МА(q ). Справедливо следующее выражение для ковариаций:

(2.28)

Автокорреляционная функция процесса МА(q) получается непосредственно из (2.28):

(2.29)

Таким образом, автокорреляционная функция r(t) процесса МА(q) равна нулю для всех значений t, больших порядка процесса q. Это важное свойство используется при подборе порядка МА(q)-модели по экспериментальным данным ;

Спектральная плотность процесса МА(q) может быть вычислена с помощью соотношения:

Идентификация модели МА(q) производится на базе соотношений (2.29), а именно: 1) по значениям с помощью формулы

подсчитываются значения ; 2) в соотношения (2.29) последовательно подставляются значения t = 1,…, q с заменой в левой их части величин r(t) полученными ранее оценками ; 3) полученная таким образом система из q уравнений разрешается относительно неизвестных значений q1,…, qq; решения этой системы и дадут оценки неизвестных параметров модели; 4) оценка параметра может быть получена с помощью первого из соотношений (2.28) подстановкой в него вместо g(0), q1,…, qq их оценок.

Заметим, что в отличие от системы уравнений Юла-Уокера (2.25), уравнения для определения оценок параметров МА(q)-модели нелинейны. Поэтому эти уравнения приходится решать с помощью итерационных процедур .

Взаимосвязь процессов AR(q) и МА(q). Сделаем ряд замечаний о взаимосвязях между процессами авторегрессии и скользящего среднего.

1. Для конечного процесса авторегрессии порядка p dt может быть представлено как конечная взвешенная сумма предшествующих e, или et может быть представлено как бесконечная сумма предшествующих d. В то же время, в конечном процессе скользящего среднего порядка q et может быть представлено как конечная взвешенная сумма предшествующих d или dt - как бесконечная взвешенная сумма предшествующих e.

2. Конечный процесс МА имеет автокорреляционную функцию, обращающуюся в нуль после некоторой точки, но так как он эквивалентен бесконечному процессу AR, его частная автокорреляционная функция бесконечно протяженная. Главную роль в ней играют затухающие экспоненты и (или) затухающие синусоиды. И наоборот, процесс AR имеет частную автокорреляционную функцию, обращающуюся в нуль после некоторой точки, но его автокорреляционная функция имеет бесконечную протяженность и состоит из совокупности затухающих экспонент и или затухающих синусоид.

Условия обратимости . Процесс скользящего среднего второго порядка определен как

и стационарен для всех значений и . Однако он обратим только тогда, когда корни характеристического уравнения

(3.3.9)

лежат вне единичного круга, т. е.

Эти условия аналогичны условиям (3.2.18) стационарности процесса АР(2)

Автокорреляционная функция . Из (3.3.3) следует, что дисперсия процесса равна

и из (3.3.4) - что автокорреляционная функция равна

(3.3.11)

Таким образом, автокорреляционная функция обрывается после задержки 2.

Из (3.3.10) и (3.3.11) вытекает, что первые две автокорреляции обратимого процесса СС(2) должны лежать внутри площади, ограниченной отрезками кривых

(3.3.12)

Область обратимости (3.3.10) для параметров процесса показана на рис. 3.8,а, и соответствующая область (3.3.12) значений автокорреляций - на рис. 3.8,б. Последний рисунок позволяет оценить, согласуется ли данная пара значений с гипотезой, что модель - процесс СС(2). Если согласие имеется, значения и можно найти, решив нелинейные уравнения (3.3.11). Для облегчения такого расчета можно использовать диаграмму в конце книги; она позволяет прямо находить значения и по данным и .

Спектр . Из (3.3.5) находим спектр

(3.3.13)

Заметим, что это спектр с точностью до постоянного множителя обратен спектру (3.2.29) процесса авторегрессии простого порядка.

Частная автокорреляционная функция. Точное выражение для функции частной автокорреляции процесса СС(2) оказывается сложным, но главную роль в нем играет либо сумма двух экспоненциальных членов [если корни характеристического уравнения (3.3.9) действительны], либо затухающая синусоида [если корни (3.3.9) комплексны]. Таким образом, эта функция ведет себя так же как, как автокорреляция процесса АР(2).

Рис. 3.8. Допустимые области значений для обратимого процесса СС(2)

Рис 3.9. Автокорреляционная и частная автокорреляционная функции для различных моделей СС(2)

На рис. 3.9 (заимствованном из ) показаны автокорреляционные функции (кривые слева) и частные автокорреляционные функции(кривые справа) для различных значений параметров из области обратимости. Сравнение с рис. 3.2, на котором приведены соответствующие автокорреляции и частные автокорреляции, иллюстрирует взаимность процессов СС(2) и АР(2).

Среди моделей для стационарных временных рядов широкое распространение имеют модели скользящей средней .

Для стационарного ряда моделируемый уровень временного ряда можно представить как линейную функцию прошлых ошибок, т.е. разностей между прошлыми фактическими и теоретическими уровнями:

где μ – константа;– белый шум в текущий и предыдущий период времени:

Термин "скользящая средняя", используемый здесь, не синоним скользящей средней как методу сглаживания уровней динамического ряда.

В модели (7.20) уровень динамического ряда рассматривается как сумма константы μ и скользящей средней между текущими и предыдущими значениями белого шума (случайных отклонений).

Обозначим скользящую среднюю модели (7.20) через :

Уравнение (7.21) принято называть процессом скользящего среднего порядка q и обозначать как МА (q) от английского Moving Average. Порядок скользящей средней определяется числом учитываемых в модели предыдущих значений случайных отклонений. Так, МА (2) можно записать как , а модель уровня динамического ряда с использованием МА (2) будет иметь вид

Соответственно модель уровня ряда с использованиемМА(1) примет вид

При q = 0 и μ =0 получаем процесс белого шума.

Временные ряды с использованием процесса скользящего среднего могут иметь место, когда уровни динамического ряда характеризуются случайной колеблемостью.

Модели ARMA

Соединение в одной модели авторегрессионного процесса AR и модели скользящего среднего МА приводит к модели авторегрессионного процесса со скользящими средними в остатках (ARMA – от английского Auto Regressive – Moving Average):

В модели (7.22) в качестве объясняющих переменных рассматриваются лаговые значения зависимой переменной ср интервалами сдвига и скользящие средние порядка q для остатков авторегрессии. Иными словами, модель включает в себя AR (р ) иМА (q). Ее принято обозначать ARMA (р, q). Например, ARMA (3, 2) имеет вид

При практической реализации моделей ARMA наиболее сложным является выбор числа лагов р и q.

Инструментом идентификации модели ARMA является изучение частной автокорреляционной функции по моделям с разным числом лагов. Частная автокорреляционная функция (PACF – Partial Autocorrelation Function ) представляет собой серию частных коэффициентов автокорреляции {РАС), которые измеряют связь между текущим уровнем динамического рядаи предыдущими значениямив условиях, когда влияние других промежуточных временных лагов устранено. Так, частный коэффициент автокорреляции при лаге к будет представлять собой корреляциюи, очищенную от влияния

Обозначим частный коэффициент автокорреляции с лагом к через. При(уровни ряда коррелируют сами с собой); при, где–коэффициент автокорреляции первого порядка. Это равенство связано с тем, что при расчете р(1) отсутствуют промежуточные лаги. Вычисление р более высокого порядка можно производить по формулам

В данных формулах определитель числителя отличается от определителя в знаменателе только заменой последнего столбцаопределителя в знаменателе столбцом из значений

Пример 7.3

За 50 мес. темпы прироста объема продукции К характеризовались авторегрессией вида и F = 93,9. Автокорреляционная функция составила убывающие значения автокорреляции:

Для модели типа МА (q) порядок q определяется по поведению автокорреляционной функции: при стремится к нулю. Для модели ARMA (р, q) автокорреляционная функция характеризуется убыванием, начинающимся с лага q, а частная автокорреляционная функция убывает, начиная с лага р. Так, для модели ARMA (1,1) приACF наблюдает экспоненциальное затухание с лага 1, a PACF – осциллирующее убывание слага 1. ПриACF для модели ARMA (1,1) наблюдает осциллирующее убывание с лага 1, a PACF – экспоненциальное затухание с лага 1.

Выбор типа модели ARMA не ограничивается обычно исследованием автокорреляционных функций. С этой целью может использоваться, например, информационный критерий Акайке1, рассмотрение которого не входит в задачу данного учебника.

Модели ARIMA

Для получения стационарного ряда могут рассчитываться разности уровней временного ряда Δ разного порядка d. Модель, в которой соединены нахождение последовательных разностей временного ряда порядка d и ARMA, – модель порядка (р, q), получила название авторегрессионной интегрированной модели скользящей средней – ARI MA (Autoregressive Integrated Moving Average).

Модель ARIMA обладает тремя параметрами: р – порядок авторегрессии AR; d – порядок последовательных разностей уровней временных рядов, обеспечивающий стационарность ряда, и q – порядок скользящей средней МА.

Итак, дело дошло до скользящего среднего (moving average , MA). Модель скользящего среднего - вещь совершенно не сложная, однако, как и все остальные модели прогнозирования или их составляющие, имеет целый ряд нюансов. Например, Википедия содержит в себе весьма громоздкое описание указанной модели , однако я не стану тут так подробно говорить об ней, но постараюсь кратко изложить основную ее идею.

Часто случается, что в исследуемом процессе имеются выбросы. Как правило, они весьма сложно исследуются. Очевидно, что подобные выбросы дурно влияют на ближайшие к ним прогнозные значения.

Ниже на графике представлен временной ряд цен рынка на сутки вперед (РСВ). Представим, что мы имеем фактические значения данного временного ряда до дня №2 и ранее, а спрогнозировать нам нужно значения в день №3. Совершенно очевидно, что если временной ряд регулярный, то выбросы дня №2 самым дурными образом скажутся на вычисленных значениях, если эти пики не сгладить.

Для сглаживания подобных пиков и применяется модель скользящего среднего , которая, по сути дела, представляет собою простой фильтр низких частот.

Скользящее среднее второго порядка, которое принято обозначать как MA(2) для временного ряда Z(t) вычисляется следующим образом:

Скользящее среднее третьего порядка MA(3) вычисляется аналогично:

Скользящее среднее пятого порядка MA(5):

Таким образом, для скользящего среднего порядка p легко написать следующую формулу:

То есть скользящее среднее для момента t является алгебраическим средним нескольких предыдущих значений исходного временного ряда Z(t) . На следующем графике представлен исходный временной ряд, а также MA(2) и MA(5). Обратите внимание на то, каким образом модель скользящего среднего влияет на выбросы в трех часах дня №2. Заметно, что выбросы существенно сгладились, однако весь остальной профиль временного ряда MA существенно не отличается от исходного, только несколько сдвинут по фазе. Такой сдвиг по фазе легко устранить обычным сдвигом значений ряда.

Таким образом, ясно, что скользящее среднее представляет собой фильтр , который позволяет сглаживать выбросы временного ряда, которые, в свою очередь, спрогнозировать достаточно сложно или вовсе невозможно.

У модели скользящего среднего множество нюансов, с которыми вы можете ознакомиться самостоятельно.