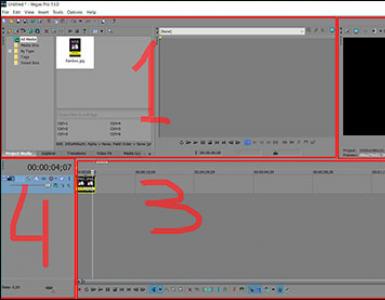
Математические модели сообщений и сигналов. Спектральные представления сигналов

Увеличение числа уплотняемых каналов без увеличения числа физических линий возможно путём наделения сигналов особыми индивидуальными признаками, которые бы приводили к различению уплотняемых каналов с целью их дальнейшего разделения. Такими признаками в обще случае могут быть параметры переносчиков сигналов: амплитуда, частота, фаза в случае непрерывной модуляции, временное положение, длительность или форма импульсов при дискретной модуляции.

Пусть необходимо организовать одновременную и независимую работу индивидуальных каналов по общему групповому тракту. Предположим, что каждый канал есть результат я балансной амплитудной или узкополосной угловой модуляции первичного сигнала, линеаризованная модель которых в упрощённой форме имеет вид

, (6.5)

где
соответственно первичный сигнал и функция переносчика-го канала,
.

Будем также полагать, что сумма верхних границ эффективно передаваемых участков спектра первичных сигналов намного меньше частотыканальных переносчиков, т.е.

для всех
. (6.6)

Сигнал группового
тракта в соответствии с формулами (6.5) и (6.2) равен

. (6.7)

Функцию модели группового сигнала можно увязать с фильтрующими свойствами дельта-функции (см. также формулу (4.9) третьей главы), а именно

где
дельта-функция;
-ый дискретный отсчёт сигнала
;
время дискретизации.

Согласно (6.7) подставим в (6.8) значения канальных сигналов
, взятые в отсчётные моменты времени
,

. (6.9)

Если считать, что в канале передачи отсутствуют искажения и помехи, то оценка группового сигнала
(см. рисунок 6.1) равна сигналу
.

На приёмной стороне системы будем наблюдать за сигналом
в течение короткого промежутка времени, также для удобства возьмём
. Так как интервалотносительно короткий, то согласно (6.6) изменение сигналов
,
будет обусловлено действием только одних переносчиков, а не первичных сигналов. Тогда можно положить, что значения первичного сигнала являются константами для выбранного промежутка времени наблюдения, т.е.

,
. (6.10)

Нетрудно видеть, что условие (6.9) будет выполняться, если будут соблюдаться система равенств по отдельным отсчётам группового сигнала:

(6.11)

Система (6.11) получена с учётом (6.10).

Выражение (6.11) может быть переписано в компактной матричной форме. Введем в рассмотрение вспомогательный вектор отсчётов группового сигнала, вектор первичных сигналови матрицу переносчиков
:

.

С учётом введенных обозначений система (6.11) будет описываться так

. (6.12)

Так как передача группового сигнала происходит без искажения, то выделение первичных сигналов осуществляется по данным отсчётов группового сигнала. При этом признаки канальных сигналов определяются матрицей переносчиков
, которая должна быть «известной» для аппаратуры разделения каналов в приёмной части многоканальной системы. Другими словами, задача разделения каналов сводится к определению вектора отсчётных значений первичных сигналовпри условии, что известными являются вектор наблюдения группового сигналаи матрица переносчиков
. Следовательно, чтобы определить векторнадо решить систему линейных уравнений (6.12). Решение (6.12) можно записать в виде

где
матрица обратная
;
единичная матрица размерности
. Как видно из (6.13), решение системы линейных уравнений (6.12) связано с обращением квадратной матрицы переносчиков
.

Из курса линейной алгебры известно, что обращение квадратной матрицы связано с вычислением её определителя. Обозначим определитель матрицы
как
. Также из теории решения линейных уравнений известно, что единственность (однозначность) решения (6.13) возможно, если

. (6.14)

Ненулевое значение определителя (6.14) возможно тогда и только тогда, когда столбцы (и строки) матрицы
линейно независимы. Условие линейной независимости столбцов формулируется так: взвешенная сумма столбцов матрицы
равна нулевому вектору, т.е.

, (6.15)

только тогда, когда числа . Если найдётся хотя бы одно число
, то определитель (6.14) будет равен нулю и система (6.12) не будет иметь единственного и однозначного решения, что говорит невозможности разделения каналов на приёмной стороне многоканальной системы.

Каждый столбец представлен в (6.15) отсчётами переносчиков -го канала. Следовательно, первое условие построения многоканальных систем связи заключается в обеспечениилинейной независимости переносчиков канальных сигналов.

Переносчики сигналов могут быть представлены непрерывными функциями времени
(
). В общем случае условие линейной независимости переносчиков канальных сигналов записывается в виде

только когда для некоторого временного интервала
, в течение которого осуществляется многоканальная передача сигналов.

Например, гармонические переносчики вида
(
) являются линейно независимыми, если будут иметь разные частотыдля каждого канала. В противном случае они будут линейно зависимыми, даже, если будут характеризоваться разными значениями амплитуд.

Как видно из формулы (6.13) для того, чтобы восстановить вектор первичного сигнала необходимо произвести обращение матрицы
, что является достаточно трудоёмкой операцией, которая усложняется при увеличении
количества каналов.

Решение уравнения (6.12) существенно упрощается, если матрица E является ортогональной, т.е. её обратная матрица равняется транспонированной матрице

и
. (6.16)

Выпишем подробнее произведение матриц
и приравняем его единичной матрице:

.

Из последнего равенства нетрудно установить новое свойство переносчиков: сумма произведения дискретных отсчётов «одноимённых» (с одним и тем же индексом одним и тем же номером канала
) переносчиков не равна нулю, а «разноимённых» (для разных индексовразных каналов
)равна нулю, т.е.

(6.17)

Свойство (6.17) определяет ортогональность переносчиков «разноимённых» канальных сигналов.

По существу левая часть выражения (6.17) в
-мерном пространстве Евклида есть скалярное произведение векторови, т.е.

, (6.18)

где
индекс транспонирования. Скалярное произведение отражает проекцию векторов друг на друга. Так, если
векторыиортогональны, то их взаимная проекция равна нулю. Если
, то сумма (6.17) и (6.18) равна квадрату длины (нормы) вектора.

Следует заметить, что если переносчики сигналов ортогональны, то решение линейной системы уравнений (6.12) резко упрощается

В общем случае, при
пространство Евклида переходит в бесконечномерное пространство Гильберта. В этом случае скалярное произведение отсчётов (6.17) заменяется скалярным произведением непрерывных функций переносчиков. Для вещественных функций переносчиков
и
принцип ортогональности на конечном временном интервале наблюдения
примет вид

. (6.20)

Для бесконечного интервала наблюдения
ортогональность непрерывных переносчиков будет иметь вид

где
некоторая весовая функция (смысл её поясняется ниже).

Представленные основы теории линейного разделения каналов были построены без учёта действия помех и искажений в каналах передачи. В этих условиях построение многоканальных систем может осуществляться без особой разницы, как из условия линейной независимости, так и условия ортогональности канальных переносчиков . Однако при наличии в каналах помех предпочтение отдаётся многоканальным системам с ортогональными переносчиками, позволяющими повысить помехоустойчивость передаваемых сигналов.

ОСНОВЫ ТЕОРИИ АНАЛИЗА СИГНАЛОВ

2.1. Элементы теории ортогональных сигналов.

2.2. Спектральный анализ периодических сигналов.

2.3. Спектральный анализ непериодических сигналов. Преобразование Фурье.

2.4. Основные свойства преобразования Фурье.

2.5. Распределение энергии в спектрах периодических и непериодических сигналов.

Теория и техника формирования и обработки сигналов предполагает разложение заданной функции по различным ортогональным системам функций. Напомним основные определения, относящиеся к свойствам ортогональных систем.

Бесконечная система действительных функций

v 0 (x), v 1 (x), v 2 (x), ..., v n (x) (2.1)

называется ортогональной на отрезке , если

при n¹m. (2.2)

При этом предполагается, что

т.е. что никакая из функций рассматриваемой системы (2.1) не равна тождественно нулю. Условие (2.2) выражает попарную ортогональность функций системы (2.1). Величина называется нормой функции v n (x). (Это понятие аналогично понятию длины вектора в математике).

Функция v n (x), для которой выполняется условие

, (2.4)

называется нормированной функцией, а система нормированных функций v 1 (x), v 2 (x), ..., в которой каждые две различные функции взаимно ортогональны, называется ортонормированной системой. Говорят, что при этом в пространстве сигналов задан ортонормированный базис .

Произвольный сигнал s(t) можно разложить в ряд в выбранном ортонормированном базисе:

(2.5)

Представление (2.5) называется обобщенным рядом Фурье сигнала s(t) в выбранном базисе. Коэффициенты этого ряда находят следующим образом. Возьмем базисную функцию v k с произвольным номером k, умножим на нее обе части равенства (2.5) и затем проинтегрируем результаты по интервалу времени, в котором заданы сигналы:

(2.6)

Ввиду ортонормированности базиса в правой части (2.6) остается только член суммы с номером i = k, поэтому

(2.7)

т.е. коэффициенты обобщенного ряда Фурье определяются как скалярные произведения разлагаемого сигнала и соответствующих базисных векторов.

Возможность представления сигналов посредством обобщенных рядов Фурье имеет принципиальное значение. Вместо изучения функциональной зависимости на несчетном множестве точек, мы получаем возможность характеризовать эти сигналы счетной (но, вообще говоря, бесконечной) системой коэффициентов обобщенного ряда Фурье, которые представляют собой проекции вектора s(t) в ортонормированном пространстве на базисные направления. Кроме этого, обобщенный ряд Фурье обладает следующим важным свойством: при заданной системе функций v n (x) и при фиксированном числе слагаемых ряда (2.5) он обеспечивает наилучшую аппроксимацию (в смысле минимума среднеквадратической ошибки) данной функции сигнала s(t).

Ортогональная система называется полной , если увеличением числа членов в ряде среднеквадратическую ошибку можно сделать сколь угодно малой. Условие полноты можно записать в виде соотношения:

(2.8)

Применительно к сигналам s(t) выражение (2.8) принимает энергетический смысл:

(2.9)

Здесь s 2 (t 0) – мгновенная мощность сигнала в данный момент времени (P=I 2 R=U 2 /R). При этом, если под s(t) подразумевается электрическое колебание (ток, напряжение), то Е есть не что иное, как энергия сигнала в промежутке (t 2 - t 1) (при условии, что сопротивление, в котором выделяется энергия, равно 1 Ом).

Таким образом, в соответствии с (2.8) энергия сигнала при использовании ортонормированной системы функций v n (t) определится как:

Смысл полученного выражения: энергия сигнала равна сумме энергий всех компонент, из которых складывается обобщенный ряд Фурье. При этом имеется в виду, что промежуток времени (t 2 - t 1), в котором определяется энергия Е, является интервалом ортогональности для системы функций v n (t).

Очевидно, что средняя за время (t 2 - t 1) мощность сигнала:

(2.11)

Выбор наиболее рациональной ортогональной системы функций определяется видом исследуемых сигналов, поставленными задачами и выбранными методами анализа (синтеза). Так, при дискретизации непрерывных сигналов используют функции вида sinc x; при цифровой обработке сигналов - кусочно-непрерывные функции Уолша. Наибольшее распространение получили тригонометрическая {cos nx, sin nx} и экспоненциальная {exp (inx)} полные ортогональные системы базисных функций. Это объясняется следующими причинами. Во-первых, гармоническое колебание является единственной функцией времени, сохраняющей свою форму при прохождении колебания через любую линейную цепь с постоянными параметрами, при этом изменяется лишь амплитуда и фаза колебания. Во-вторых, разложение сложного сигнала по синусам и косинусам позволяет использовать символический метод, разработанный для анализа передачи гармонических колебаний через линейные цепи. Поэтому гармонический анализ получил широкое распространение во всех отраслях современной науки и техники.

7 страниц (Word-файл)

Посмотреть все страницы

Ортогональные сигналы

1. Скалярное произведение сигналов.

2. Ортогональные сигналы и обобщенные ряды Фурье.

3. Примеры ортонормированных базисов.

4. Энергия сигнала, представленная в виде обобщенного ряда Фурье.

5.Апаратурная реализация разложения сигнала по ортонормированному базису.

Рассмотрев структуру ЛПС, определив норму и метрику, мы пока лишены возможности вычислить угол между векторами, это удается при введении скалярного произведения сигналов.

c=(a,b)=|a|*|b|cosφ

1. Если в обычном декартовом пространстве известны два вектора, то:

По аналогии вычислим энергию суммы двух сигналов U и V:

Сигналы U и V аддитивны, а их энергии нет. Энергия суммарного сигнала содержит в себе некую взаимную энергию:

Сравнивая (2) и (1) определяем скалярное произведение сигналов U и V:

(3)

а также (4)

Свойства скалярного произведения сигналов (5):

3) (λU,V)=λ(U,V), λ – вещественное число.

4) (U+V,W)=(U,W)+(W,V).

ЛПС в котором введено скалярное произведение (3), при этом условия (5) – справедливы, то оно называется вещественным гильбертовым пространством H.

В гильбертовом пространстве справедливо неравенство Коши-Буняковского:

|(U,V)|≤||U||*||V|| (6)

Для комплексного гильбертового пространства скалярное произведение:

Пример: имеем 2 смещенных во времени экспоненциальных импульса напряжения:

Найти скалярное произведение сигналов и , и угол между ними:

=1.25* (*c ) .

(*c ) .

(*c).

2. Два сигнала U, V – ортогональны, если их скалярное произведение и взаимная энергия равны нулю.

То есть ортогональные сигналы предельно не похожи друг на друга.

Ортонормированный базис.

Пусть H – это гильбертовое пространство сигналов (ГПС) с конечным значением энергии. Эти сигналы определены на промежутке , конечном или бесконечном. Пусть на этом же интервале определена бесконечная система функций {U1, U2, …, Un, …} попарно ортогональных друг другу, обладающих единичными нормами. Это означает, что

(9)

Следовательно, говорят, что при этом в ГПС задан ортонормированный базис.

Произвольный сигнал S(t), пренадлежащий H, можно разложить в следующий ряд:

(10)

Получили обобщенный ряд Фурье.

Отыщем коэффициент ряда (10): C1, C2, …:

возьмем базисную функцию φ k . Умножим на нее обе части (10) и проинтегрируем обе части по заданному интервалу .

В следствии ортонормированности базиса правая часть (11) равняется Ck.

Из формулы (12) следует алгоритм вычисления коэффициентов C1, C2, … обобщенного ряда Фурье (ОРФ).

Представления сигналов ОРФ освобождает нас от необходимости изучать функциональную зависимость в несчетном множестве точек и дает право характеризовать эти сигналы коэффициентами C1, C2, …, которые являются проекциями вектора S(t) на базисные направления ГПС.

3. а) ортонормированная система гармонических сигналов на интервале (13):

Разложение периодической функции в ряды Фурье по этой ортонормированной системе будет рассмотрено далее.

б) система функций Уолта.

Эта система, графики которой на рисунке 1, являются ортонормированными:

На интервале своего существования {-π/2;π/2} они принимают лишь значения +1 и -1, отличающиеся лишь знаками.

θ=t/T – безразмерное время. k–я функция – функция Уолта, обозначается wal(k, θ).

Прежде чем рассматривать общий случай когерентного приема, полезно и поучительно остановиться на частном слуяае ортогональных сигналов. Если при всех , получается существенное упрощение выражения для вероятности ошибки, так как в этом случае корреляционная матрица превращается в единичную (8.8) и переходит в следующее соотношение:

Заметим, что формула (8.9) представляет и общую вероятность ошибки, так как представляет просто переменную интегрирования и, следовательно, не зависит от переданного сигнала.

В § 8.1 были рассмотрены два примера ортогональных сигналов, соответствующих дискретной фазово-импульсной модуляции и дискретной частотной функции. Предположим, что время передачи сигнала равно Т, а мощность сигнала S. Тогда энергия сигнала

Каждый сигнал передает символов сообщения. Так как по предположению все символы независимы и с равной вероятностью могут быть нулями и единицами, то безошибочному приему сигнала соответствует прием k бит информации. Следовательно, скорость передачи информации,

которую обозначим R, равна

С помощью (8.10) и (8.11) можно выразить основной параметр через отношение сигнал/шум , скорость передачи R и число сигналов М:

При сравнении качества двух систем связи с различным числом передаваемых сигналов разумно предполагать одинаковые значения отношения и R и не одинаковые значения отношения . На рис. 8.3 показана зависимость вероятности ошибки от при . Кривые были построены на основании результатов численного интегрирования (8.9) с помощью вычислительной машины IBM 704 .

Вероятность ошибки представляет вероятность неправильного приема последовательности из k бит, т. е. вероятность того, что появится ошибка в одной или нескольких битах из последовательности k бит. Сравним эти соотношения с соотношениями для когерентной двоичной системы связи, рассмотренной в § 7.1. Предположим, что с помощью такой системы были переданы k последовательных бит. Было показано, что вероятность ошибки при приеме любого одного бита равна , где Е - энергия сигнала и - скалярное произведение сигнала . Так как передается только один бит, то . Для того чтобы минимизировать ошибку, необходимо применить противоположные сигналы, так что . Наконец, вероятность правильного приема k последовательных бит равна k-й степени вероятности правильного приема одного бита. Следовательно, вероятность ошибки в одном или нескольких последовательных битах из переданных k бит при применении двоичной когерентной системы связи и использовании противоположных сигналов равна

(см. скан)

Рис. 8.3. Вероятность ошибки для ортогональных сигналов (k = 1, 2.....10, 15, 20).

Этот случай назовем некодированной передачей. На рис. 8.4 и 8.5 показаны для сравнения вероятности ошибок при некодированной передаче и при кодированной передаче с ортогональными сигналами для k = 5 и 10, вычисленные согласно (8.13) и (8.9) соответственно. Из рисунков видно, что при фиксированных значениях необходимая мощность сигнала уменьшается почти в два раза при и почти в четыре раза при . Другими словами, при фиксированных значениях и применение кодирования дает возможность приблизительно удвоить скорость передачи данных при и учетверить ее при k = 10.

Вероятность ошибочного приема последовательности можно принять за меру качества, например, в случае передачи сообщений, состоящих из k бит и соответствующих символам телетайпа или квантованным выборочным данным. С другой стороны, если передается последовательность независимых бит то нужно определить вероятность ошибочной передачи определенного бита. Если при ортогональных сигналах произошла ошибка, то может быть выбрано с одинаковой вероятностью решение о неправильности любого из сигналов. Это следует из того, что скалярные произведения всех пар сигналов равны (в рассматриваемом случае равны нулю). Таким образом, если произошла ошибка, то вероятность того, что искажены i из k бит, равна Следовательно, среднее число искаженных бит равно