Матрицы и проекции в opengl. Программирование с использованием DirectX9: Вращение объектов
Графический вывод обычно осущестсвляется в некоторую прямоугольную область экрана или окна. В OpenGL-визуализации эта область называется порт вывода. Именно в этой прямоугольной области будет размещено библиотекой сформированное изображение. Его размеры определяются относительно левого верхнего угла окна и измеряются в пикселах. Для определения порта вывода приложение должно отследить событие изменения размеров окна и определить порт вывода с использованием функции:
void glViewport(GLint x, GLint y, GLsizei width, GLsizei height);
Аргументы (x, y) определяют положение верхнего левого угла порта вывола, а width и height -- его размеры. По умолчанию библиотека растягивает порт вывода на всё OpenGL-окно.
Координатная система
Прежде чем быть отображённой на экране вершина, заданная в системе координат сцены должна пройти процесс проецирования. Для описания и проведения преобразований систем координат в библиотеке OpenGL используется матричный аппарат. Сама система координат и ее преобразования описываются матрицами в так называемых однородных координатах.
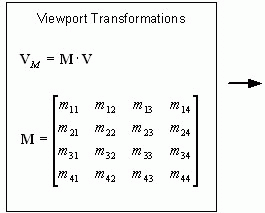
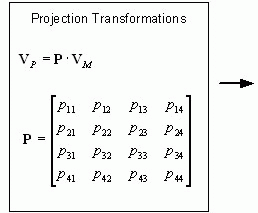
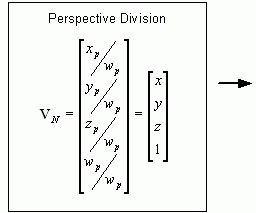
Во-первых, вершина преобразуется в матрицу 1X4, в которой первые три элемента представляют собой координаты x, y, z. Четвёртое число - масштабный коэффициент w, который обычно равен 1.0. Вершина домножается на видовую матрицу, которая описывает преобразования видовой системы координат. Получаем вершину в координатах вида. Она в свою очередь домножается на матрицу проекций и получаем вершину в координатах проекции. На этом этапе некоторве вершины отбрасываются (из-за непопадания в объём визуализации). Затем вершины нормализуются для передачи перспективы (если координата w не равна 1.0). Окончательное проецирование вершины на двумерную поверхность экрана выполняется библиотекой OpenGL самостоятельно и вмешаться в этот процесс нельзя.
Матрица проекций
Матрица проекций отвечает за то, какой объём пространства будет визуализироваться, каким образом вершины графических примитивов будут спроецированы на двумерную поверхность экрана монитора. Преобразования матрицы проекций ведут к тому, что все изображение будет изменяться (масштабироваться, перемещаться или вращаться). В OpenGL возможно использование двух режимов матрицы проекций: перспективная и ортографическая.
При перспективной проекции используется тот факт, что для человеческий глаз работает с предметом дальнего типа, размеры которого имеют угловые размеры. Чем дальше объект, тем меньше он нам кажется. Таким образом, объём пространства, который визуализируется представляет собой пирамиду.

Матрица преспективной проекции определяется с использованием функции:
void glFrustum(GLdouble left, GLdouble right, GLdouble bottom, GLdouble top, GLdouble near, GLdouble far);
(left, bottom, -near) и (right, top, -near) определяют координаты ближней отсекающей рамки; near и far имеют всегда положительные значения и определяют расстояние от точки зрения до ближней и дальней отсекающих рамок.
Для задания матрицы перспективной проекции также можно использовать функцию gluPerspective(), которая имеет другие аргументы
void gluPerspective(GLdouble fovy, GLdouble aspect, GLdouble near, GLdouble far);

Аргумент fovy (field of view) определяет поле зрения, а aspect -- отношение ширины отсекающей рамки к высоте. near и far имеют всегда положительные значения и определяют расстояние от точки зрения до ближней и дальней отсекающих рамок.
Перспективное проецирование обычно используется в играх и приложениях, где требуется добиться высокой реалистичности объектов, подожей на визуализацию глазом. Для двумерной и трехмерной визуализации научных и технических данных обычно используется ортографическая проекция. Рассмотрим установку ортографической проекции сначала для двумерной визуализации. При ортографической проекции объём пространства, который визуализируется представляет собой параллелепипед:

Особенностями ортографической проекции является то, что расстояние от камеры до объектов не влияет на итоговое изображение.
Для установки и последующего изменения матрицы проекций следует выполнить функцию glMatrixMode(GL_PROJECTION). Для начала также следует отменить все предыдущие установки и преобразования, сделав матрицу проекций единичной с помошью функции glLoadIdentity(). Матрица ортографической проекции устанавливается с использованием функции, которая имеет следующий прототип:
void glOrtho(GLdouble left, GLdouble right, GLdouble bottom, GLdouble top, GLdouble near, GLdouble far);
(left, bottom, -near) и (right, top, -near) -- точки, определяющие ближнюю отсекающую рамку. (left, bottom, -far) и (right, top, -far) -- точки, определяющие дальнюю отсекающую рамку. После применения этой команды направление проецирования параллельно оси z в сторону отрицательных значений
//Функция изменения размеров и установки координат
void Reshape(int width, int height)
{
//Установка порта вывода
glViewport(0, 0, width, height);
//Режим матрицы проекций
glMatrixMode(GL_PROJECTION);
//Единичная матрица
glLoadIdentity();
//Установка двумерной ортографической системы координат
glOrtho(-50., 50., -50., 50., -1., 1.);
//Режим видовой матрицы
glMatrixMode(GL_MODELVIEW);
}
Специально для двумерной визуализации можно использовать функцию, которая имеет следующий прототип:
void gluOrtho2D(GLdouble left, GLdouble right, GLdouble bottom, GLdouble top);
Эта функция аналогична glOrtho(), при вызове которой аргумент near=-1.0, а far=1.0. В процессе двумерной визуализации z-координата у вершин имеет значение 0, то есть объекты находятся на средней плоскости.
При необходимости сохранения пропорций установку системы координат необходимо осуществлять с учетом отношения ширины и высоты окна.
//Установка ортографической системы координат
double aspect=width/double(height);
if(width>=height)
{
gluOrtho2D(-50.*aspect, 50.*aspect,
-50., 50.);
}
else
{
gluOrtho2D(-50., 50., -50./aspect,
50./aspect);
}
Видовая матрица
Видовая матрица отвечает за систему координат создаваемой трехмерной модели. В процессе создания модели видовая матрица может многократно изменяться для того, чтобы видоизменить изображение отдельных графических примитивов (превратить квадрат в прямоугольник, куб в параллелепипед, сферу в эллипсоид). Для установки и последующего изменения видовой матрицы следует выполнить функцию glMatrixMode(GL_MODELVIEW). Для начала также следует отменить все предыдущие установки и преобразования, сделав матрицу проекций единичной с помошью функции glLoadIdentity(). Если координаты вершин объекта задаются при его создании, то дополнительные преобразования системы координат не требуются. Однако часто это сложно или просто невозможно.
OpenGL предоставляет три функции для выполнения преобразования системы координат: glTranslated(), glRotated() и glScaled(). Эти команды генерируют матрицы переноса, поворота и масштабирования, которые домножаются на видовую матрицу с помощью функции glMultMatrix(). Как видите OpenGL берёт на себя матричные операции и выполняет их по специальным, быстрым алгоритмам с максимальной эффективностью. Например:
Перенос
Если аргумент больше 0, то объект при отображении будет смещён в сторону положительных значений вдоль оси. Если аргумент меньше 0, то объект при отображении будет смещён в сторону отрицательных значений вдоль оси.
Масштабированиe
Осуществляется с использованием функции, которая имеет следующий прототип:
Если аргумент больше 1, то объект при отображении будет увеличенным. Если аргумент меньше 1, то объект при отображении будет уменьшенным. Если аргумент отрицательный, то объект при отображении будет ещё и отраженным. Нулевое значение аргумента допускается, но будет приводить ктому, что размеры объекта будут нулевыми.
Поворот
Осуществляется с использованием функции, которая имеет следующий прототип:
| void glRotated(double angle, double x, double y, double
z);
glRotated(30.,0.,0.,1.); //Поворот вокруг z glBegin(GL_LINE_LOOP); //Установка вершин glVertex2d(-2., 2.); glVertex2d(2., 2.); glVertex2d(2., -2.); glVertex2d(-2., -2.); glEnd(); |
 |
 |
Первый аргумент определяет угол поворота, а остальные три -- координаты вектора, вокруг которого осуществляется вращение.
Стек матриц
Полезным механизмом при построении сложных изображений является стек матриц. С использованием функций glPushMatrix() и glPopMatrix() можно запомнить текущую матрицу в стеке и восстановить ее после каких либо изменений в системе координат.
Дисплейные списки
Интересным и очень эффективным механизмом при создании сцены являются списки. Это механизм, который позволяет запоминать последовательности команд OpenGL и выполнять их снова. Это может существенно повысить эффективность визуализации большого количества одинаковых объектов.
Каждый дисплейный список должен иметь идентификатор. Это может быть произвольное целое число, которое вы можете назначить сами. Во избежание конфликтов идентификаторов списков библиотека OpenGL рекомендует воспользоваться функцией
GLuint glGenLists(GLsizei range);
которая находит свободный идентификатор и возвращает его. В качестве аргумента функции указывается количество, следующих подряд, списков, для которых следует получить идентификаторы. Если свободных идентификаторов не осталось, то функция возвращает ноль.
Для того, чтобы начать формировать список, необходимо вызвать функцию
void glNewList (GLuint list, GLenum mode);
Первый аргумент задает идентификатор формируемого списка, а второй определяет будет ли список только сформирован (GL_COMPILE) или сразу же и отображен (GL_COMPILE_AND_EXECUTE). Далее могут следовать команды OpenGL которые требуется сохранить в списке. Не все команды могут быть в него включены.
Формирование списка заканчивается функцией:
void glEndList (void);
После формирования дисплейные списки сохраняются во внутренней структуре данных OpenGL-окна и будут удалены, когда окно будет закрыто или разрушено.
Для выполнения дисплейного списка используется команда:
void glCallList (GLuint list);
которая в качестве аргумента принимает идентификатор списка.
Вызов функции glCallList() можно осуществить в любом мемте программы, когда требуется выполнение сохраненных в списке команд.
Рассмотрим пример:
| void Draw(void) { //Очистка цветового буфера glColor3d(1.0, 1.0, 0.0); glBegin(GL_LINES); glVertex2d(-50., .0); glVertex2d(50., .0); For(int i=-50; i<50;
i++) |
void Draw(void) { //Очистка цветового буфера glClear(GL_COLOR_BUFFER_BIT); //Установка цвета отображения glColor3d(1.0, 1.0, 0.0);
//Формирование оси For(int i=0.; i<97; i++)
//Рисование вертикальной оси //Завершить выполнение команд |
Двигатель не двигает
корабль.
Корабль остается на
месте, а
двигатели двигают вселенную
вокруг него.
Футурама
Это один из самых важных уроков. Вдумчиво прочитайте его хотя бы восемь раз.
Гомогенные координаты
В предыдущих уроках мы предполагали, что вершина расположена по координатам (x, y, z). Давайте-ка добавим еще одну координату – w. Отныне вершины у нас будут по координатам (x, y, z, w)
Вскоре вы поймете, что к чему, но пока примите это как данность:
- Если w==1, тогда вектор (x,y,z,1) – это позиция в пространстве
- Если w==0, тогда вектор (x,y,z,0) – это направление.
Запомните это как аксиому без доказательств!!!
И что это нам дает? Ну, для вращения ничего. Если вы вращаете точку или направление, то получите один и тот же результат. Но если вы вращаете перемещение(когда вы двигаете точку в определенном направлении), то все кардинально меняется. А что значит «переместить направление»? Ничего особенного.
Гомогенные координаты позволяют нам оперировать единым матаппаратом для обоих случаев.
Матрицы Трансформаций
Введение в матрицы
Если по простому, то матрица, это просто массив чисел с фиксированным количеством строк и столбцов.
Например, матрица 2 на 3 будет выглядеть так:
В 3д графике мы пользуемся почти всегда матрицами 4х4. Это позволяет нам трансформировать наши (x,y,z,w) вершины. Это очень просто – мы умножаем вектор позиции на матрицу трансформации.
Матрица*Вершину = трансформированная вершина
Все не так страшно как выглядит. Укажите пальцем левой руки на a, а пальцем правой руки на x. Это будет ax. Переместите левый палец на следующее число b, а правый палец вниз на следующее число – y. У нас получилось by. Еще раз – cz. И еще раз – dw. Теперь суммируем все получившиеся числа – ax+by +cz +dw . Мы получили наш новый x. Повторите то же самое для каждой строки и вы получите новый вектор (x,y,z,w).
Однако это довольно скучная операция, так что пусть её за нас будет выполнять компьютер.
В С++ при помощи библиотеки GLM:
glm::mat4 myMatrix;
glm::vec4 myVector;
glm :: vec 4 transformedVector = myMatrix * myVector ; // Не забываем про порядок!!! Это архиважно!!!
В GLSL:
mat4 myMatrix;
vec4 myVector;
// заполняем матрицу и вектор нашими значениями… это мы пропускаем
vec 4 transformedVector = myMatrix * myVector ; // точно так же как и в GLM
(Чего-то мне кажется, что вы не скопировали этот кусок кода к себе в проект и не попробовали…ну же, попробуйте, это интересно!)
Матрица перемещений
Матрица перемещения, это, наверное, самая простая матрица из
всех. Вот она:

Тут X, Y, Z – это значения, которые мы хотим добавить к нашей позиции вершины.
Итак, если нам нужно переместить вектор (10,10,10,1) на 10
пунктов, по позиции Х, то:
(Попробуйте это сами, ну пожаааалуйста!)
…И у нас получится (20,10,10,1) в гомогенном векторе. Как вы, я надеюсь, помните, 1 значит, что вектор представляет собой позицию, а не направление.
А теперь давайте попробуем таким же образом трансформировать
направление (0,0,-1,0):
И в итоге у нас получился тот же вектор (0,0,-1,0).
Как я и говорил, двигать направление не имеет
смысла.
Как же нам закодить это?
В С++ при помощи GLM:
#include
glm::mat4 myMatrix = glm::translate(10.0f, 0.0f, 0.0f );
glm::vec4 myVector(10.0f, 10.0f, 10.0f, 0.0f );
glm :: vec 4 transformedVector = myMatrix * myVector ; // и какой у нас получится результат?
А в GLSL: В GLSL так редко кто делает. Чаще всего с помощью функции glm::translate(). Сначала создают матрицу в С++, а затем отправляют её в GLSL, и уже там делают лишь одно умножение:
vec4 transformedVector = myMatrix * myVector;
Единичная матрица(Identity Matrix)
Это специальная матрица. Она не делает ничего. Но я упоминаю её, так как важно знать, что умножение A на 1.0 в результате дает А:
glm::mat4 myIdentityMatrix = glm::mat4(1.0f);
Матрица Масштабирования
Матрица масштабирования так же достаточно проста:
Поэтому если вам хочется увеличить вектор(позицию или направление, не важно) в два раза по всем направлениям:
А координата w не поменялась. Если вы спросите: «А что такое масштабирование направления?». Полезно не часто, но иногда полезно.
(заметьте, что масштабирование единичной матрицы с (x,y,z) = (1,1,1))
С++:
//
Используйте
#include
glm::mat4 myScalingMatrix = glm::scale(2.0f, 2.0f ,2.0f);
Матрица Вращения
А вот эта матрица достаточно сложная. Поэтому я не буду останавливаться на подробностях её внутренней реализации. Если сильно хочется, лучше почитайте (Matrices and Quaternions FAQ)
В С ++:
//
Используйте
#include
glm::vec3 myRotationAxis(??, ??, ??);
glm::rotate(angle_in_degrees, myRotationAxis);
Совмещенные Трансформации
Теперь мы знаем как вращать, перемещать и масштабировать наши вектора. Хорошо бы узнать, как объединить все это. Это делается просто умножением матриц друг на друга.
TransformedVector = TranslationMatrix * RotationMatrix * ScaleMatrix * OriginalVector;
И снова порядок!!! Сначала нужно изменить размер, потом прокрутить и лишь потом сдвинуть.
Если мы будем применять трансформации в другом порядке, то не получим такой же результат. Вот попробуйте:
- Сделайте шаг вперед(не свалите компьютер со стола) и повернитесь влево
- Повернитесь влево и сделайте один шаг вперед.
Да, нужно всегда помнить про порядок действий при управлении, например, игровым персонажем. Сначала, если нужно, делаем масштабирование, потом выставьте направление(вращение) а потом перемещайте. Давайте разберем небольшой пример(я убрал вращение для облегчения расчетов):
Не правильный способ:
- Перемещаем корабль на (10,0,0). Его центр теперь на 10 по Х от центра.
- Увеличиваем размер нашего корабля в 2 раза. Каждая координата умножается на 2 относительно центра который далеко… И в итоге у нас получается корабль необходимого размера но по позиции 2*10=20. Что не совсем то, чего мы хотели.
Правильный способ:
- Увеличиваем размер корабля в 2 раза. Теперь у нас есть большой корабль расположенный по центру.
- Перемещаем корабль. Размер корабля не изменился и он расположен в нужном месте.
ВС++:
glm::mat4 myModelMatrix = myTranslationMatrix * myRotationMatrix * myScaleMatrix;
glm::vec4 myTransformedVector = myModelMatrix * myOriginalVector;
В GLSL:
mat4 transform = mat2 * mat1;
vec4 out_vec = transform * in_vec;
Матрицы Модели, Вида и Проекции
Для иллюстраций предполагаем, что мы уже умеем рисовать в OpenGL любимую 3д модель программы Blender – голову обезьяны Сюзанны.Матрицы Модели, Вида и Проекции очень удобный метод разделения трансформаций. Если сильно хочется, вы можете не использовать их(мы же не использовали их в уроках 1 и 2). Но я настойчиво рекомендую вам пользоваться ими. Просто почти все 3д библиотеки, игры итд используют их для разделения трансформаций.
Матрица Модели
Данная модель, как и наш любимый треугольничек, задана набором вершин. X, Y, Z координаты заданы относительно центра объекта. Так вот, если вершина расположена по координатам (0,0,0), то она находится в центре всего объекта
Теперь мы имеем возможность двигать нашу модель. Например,
потому, что пользователь управляет ей с помощью клавиатуры и мыши. Это сделать
очень просто: масштабирование*вращение*перемещение и все. Вы применяете вашу
матрицу ко всем вершинам в каждом кадре(в GLSL а не в C++) и все перемещается. Все
что не перемещается – расположено в центре «мира».

Вершины находятся в мировом пространстве Черная стрелка на рисунке показывает, как мы переходим из пространства модели, в мировое пространство(Все вершины были заданы относительно центра модели, а стали заданы относительно центра мира)

Эту трансформацию можно отобразить следующей диаграммой:

Матрица Вида
Давайте еще раз прочитаем цитату из футурамы:«Двигатель не двигает корабль. Корабль остается на месте, а
двигатели двигают вселенную вокруг него.»

То же самое можно применить и к фотоаппарату. Если вы хотите сфотографировать гору под каким-нибудь углом, то можно передвинуть фотокамеру…или гору. В реальной жизни это невозможно, но очень легко и удобно в компьютерной графике.
По умолчанию наша камера находится в центре Мировых Координат. Чтобы двигать наш мир нужно создать новую матрицу. К примеру нам нужно переместить нашу камеру на 3 единицы вправо(+Х). Это то же самое, что переместить весь мир на 3 единицы влево(-Х). И пока ваши мозги плавятся, давайте попробуем:
// Используйте #include
glm::mat4 ViewMatrix = glm::translate(-3.0f, 0.0f ,0.0f);
Картинка ниже демонстрирует это: мы переходим от Мирового
пространства(все вершины заданы относительно центра мира как мы это делали в
предыдущей секции) к пространству камеры(все вершины заданы относительно
камеры).

И прежде чем ваша голова совсем взорвется, посмотрите на прекрасную функцию из нашей старой доброй GLM:
glm::mat4 CameraMatrix = glm::LookAt(
cameraPosition , // Позиция камеры в мировых координатах
cameraTarget , // точка на которую мы хотим посмотреть в мировых координатах
upVector // скорее всего glm :: vec 3(0,1,0), а (0,-1,0) будет все показывать вверх ногами, что иногда тоже прикольно.
Вот иллюстрация к вышесказанному:

Но к нашей радости, это еще не все.
Матрица Проекции
Сейчас мы имеем координаты в пространстве камеры. Это значит, что после всех этих трансформаций, вершина которой посчастливилось оказаться в x==0 и y==0 будет отрендерена в центре экрана. Но мы же не можем пользоваться лишь координатами X,Y, чтобы понять куда рисовать вершину: дистанция к камере(Z) должна тоже учитываться! Если у нас есть две вершины, то одна из них будет более ближе к центру экрана чем другая, так как у неё больше координата Z.Это называется перспективная проекция:

И к большому счастью для нас, матрица 4х4 может представлять собой и перспективные трансформации:
glm::mat4 projectionMatrix = glm::perspective(
FoV , // Горизонтальное Поле Вида в градусах. Или величина приближения . Как будто « линза » на камере . Обычно между 90(суперширокий, как рыбий глаз) и 30(как небольшая подзорная труба)
4.0 f / 3.0 f , // Соотношение сторон. Зависит от размера вашего окна. Например, 4/3 == 800/600 == 1280/960, знакомо, не правда ли?
0.1 f , // Ближнее поле отсечения. Его нужно задавать как можно большим, иначе будут проблемы с точностью.
100.0 f // Дальнее поле отсечения. Нужно держать как можно меньшим.
);
Повторим то что мы сейчас сделали:
Мы ушли от пространства камеры(все вершины заданы в координатах относительно камеры) в гомогенное пространство(все вершины в координатах маленького куба(-1,1). Все что находится в кубе – находится на экране.)
И финальная диаграмма:

Вот еще одна картинка чтобы стало яснее, что же происходит,
когда мы умножаем всю эту проекционную матричную ерунду. Перед умножением на
проекционную матрицу у нас есть голубые объекты заданные в пространстве камеры
и красный объект, который представляет собой поле вида камеры: пространство
которое попадает в объектив камеры:

После умножения на проекционную матрицу у нас выходит
следующее:

На предыдущей картинке поле вида превратилось в идеальный куб(с координатами вершин от -1 до 1 по всем осям.), а все объекты деформированы в перспективе. Все голубые объекты которые близко к камере – стали большими, а которые дальше – маленькими. Так же как и в жизни!
Вот какой вид у нас открывается из «объектива»:

Однако оно квадратное, и нужно применить еще одно математическое преобразование, чтобы подогнать картинку под размеры окна.
В определённый момент у любого разработчика в области компьютерной графики возникает вопрос: как же работают эти перспективные матрицы? Подчас ответ найти очень непросто и, как это обычно бывает, основная масса разработчиков бросает это занятие на полпути.
Это не решение проблемы! Давайте разбираться вместе!
Будем реалистами с практическим уклоном и возьмём в качестве подопытного OpenGL версии 3.3. Начиная с этой версии каждый разработчик обязан самостоятельно реализовывать модуль матричных операций. Замечательно, это то, что нам нужно. Проведём декомпозицию нашей с вами нелёгкой задачи и выделим основные моменты. Немного фактов из спецификации OpenGL:
- Матрицы хранятся по столбцам (column-major);
- Однородные координаты;
- Канонический объём отсечения (CVV) в левосторонней системе координат.
Однородные координаты – это не очень хитрая система с рядом простых правил по переводу привычных декартовых координат в однородные координаты и обратно. Однородная координата это матрица-строка размерности . Для того чтобы перевести декартову координату в однородную координату необходимо x
, y
и z
умножить на любое действительное число w
(кроме 0). Далее необходимо записать результат в первые три компоненты, а последний компонент будет равен множителю w
. Другими словами:
- декартовы координаты
w
– действительное число, не равное 0 - однородные координаты
Небольшой трюк: Если w
равно единице, то всё что нужно для перевода, это перенести компоненты x
, y
и z
и приписать единицу в последний компонент. То есть получить матрицу-строку:
Несколько слов о нуле в качестве w
. С точки зрения однородных координат это вполне допустимо. Однородные координаты позволяют различать точки и вектора. В декартовой же системе координат такое разделение невозможно. - точка, где (x, y, z
) – декартовы координаты
- вектор, где (x, y, z
) – радиус-вектор
Обратный перевод вершины из однородных координат в декартовы координаты осуществляется следующим образом. Все компоненты матрицы-строки необходимо разделить на последнюю компоненту. Другими словами: - однородные координаты
- декартовы координаты
Главное что необходимо знать, что все алгоритмы OpenGL по отсечению и растеризации работают в декартовых координатах, но перед этим все преобразования производятся в однородных координатах. Переход от однородных координат в декартовы координаты осуществляется аппаратно.
Канонический объём отсечения или Canonic view volume (CVV) – это одна из мало документированных частей OpenGL. Как видно из рис. 1 CVV – это выровненный по осям куб с центром в начале координат и длиной ребра равной двойке. Всё, что попадает в область CVV подлежит растеризации, всё, что находится вне CVV игнорируется. Всё, что частично выходит за границы CVV, подлежит алгоритмам отсечения. Самое главное что надо знать - система координат CVV левосторонняя!
Рис. 1. Канонический объём отсечения OpenGL (CVV)
Левосторонняя система координат? Как же так, ведь в спецификации к OpenGL 1.0 ясно написано, что используемая система координат правосторонняя? Давайте разбираться.
Рис. 2. Системы координат
Как видно из рис. 2 системы координат различаются лишь направлением оси Z . В OpenGL 1.0 действительно используется правосторонняя пользовательская система координат. Но система координат CVV и пользовательская система координат это две совершенно разные вещи. Более того, начиная с версии 3.3, больше не существует такого понятия как стандартная система координат OpenGL. Как упоминалось ранее, программист сам реализует модуль матричных операций. Формирование матриц вращения, формирование проекционных матриц, поиск обратной матрицы, умножение матриц – это минимальный набор операций, входящих в модуль матричных операций. Возникает два логичных вопроса. Если объём видимости это куб с длиной ребра равной двум, то почему сцена размером в несколько тысяч условных единиц видна на экране? В какой момент происходит перевод пользовательской системы координат в систему координат CVV. Проекционные матрицы – это как раз та сущность, которая занимается решением этих вопросов.
Главная мысль вышеизложенного – разработчик сам волен выбрать тип пользовательской системы координат и должен корректно описать проекционные матрицы. На этом с фактами об OpenGL закончено и подошло время сводить всё воедино.
Одна из наиболее распространённых и сложно постигаемых матриц – это матрица перспективного преобразования. Так как же она связана с CVV и пользовательской системой координат? Почему объекты с увеличением расстояния до наблюдателя становятся меньше? Для того чтобы понять почему объекты уменьшаются с увеличением расстояния, давайте рассмотрим матричные преобразования трёхмерной модели шаг за шагом. Не секрет, что любая трёхмерная модель состоит из конечного списка вершин, которые подвергаются матричным преобразованиям совершенно независимо друг от друга. Для того чтобы определить координату трёхмерной вершины на двухмерном экране монитора необходимо:
- Перевести декартову координату в однородную координату;
- Умножить однородную координату на модельную матрицу;
- Результат умножить на видовую матрицу;
- Результат умножить на проекционную матрицу;
- Результат перевести из однородных координат в декартовы координаты.
Теперь переходим к шагу три. Здесь начинает работу видовое пространство. В этом пространстве координаты отсчитываются относительно положения и ориентации наблюдателя так, как если бы он являлся центром мира. Видовое пространство является локальным относительно мирового пространства, поэтому координаты в него надо вносить (а не выносить, как в предыдущем случае). Прямое матричное преобразование выносит координаты из некоторого пространства. Чтобы наоборот внести их в него, надо матричное преобразование инвертировать, поэтому видовое преобразование описывается обратной матрицей. Как же получить эту обратную матрицу? Для начала получим прямую матрицу наблюдателя. Чем характеризуется наблюдатель? Наблюдатель описывается координатой, в которой он находится, и векторами направления обзора. Наблюдатель всегда смотрит в направлении своей локальной оси Z . Наблюдатель может перемещаться по сцене и осуществлять повороты. Во многом это напоминает смысл модельной матрицы. По большому счёту так оно и есть. Однако, для наблюдателя операция масштабирования бессмысленна, поэтому между модельной матрицей наблюдателя и модельной матрицей трёхмерного объекта нельзя ставить знак равенства. Модельная матрица наблюдателя и есть искомая прямая матрица. Инвертировав эту матрицу, мы получаем видовую матрицу. На практике это означает, что все вершины в глобальных однородных координатах получат новые однородные координаты относительно наблюдателя. Соответственно, если наблюдатель видел определённую вершину, то значение однородной координаты z данной вершины в видовом пространстве точно будет положительным числом. Если вершина находилась за наблюдателем, то значение её однородной координаты z в видовом пространстве точно будет отрицательным числом.
Шаг четыре - это самый интересный шаг. Предыдущие шаги были рассмотрены так подробно намеренно, чтобы читатель имел полную картину о всех операндах четвёртого шага. На четвёртом шаге однородные координаты выносятся из видового пространства в пространство CVV. Ещё раз подчеркивается тот факт, что все потенциально видимые вершины будут иметь положительное значение однородной координаты z .
Рассмотрим матрицу вида:
И точку в однородном пространстве наблюдателя:
Произведём умножение однородной координаты на рассматриваемую матрицу:
Переведём получившиеся однородные координаты в декартовы координаты:
Допустим, есть две точки в видовом пространстве с одинаковыми координатами x и y , но разными координатами z . Другими словами одна из точек находится за другой. Из-за перспективного искажения наблюдатель должен увидеть обе точки. Действительно, из формулы видно, что из-за деления на координату z , происходит сжатие к точке начала координат. Чем больше значение z (чем дальше точка от наблюдателя), тем сильнее сжатие. Вот и объяснение эффекту перспективы.
В спецификации OpenGL сказано, что операции по отсечению и растеризации выполняются в декартовых координатах, а процесс перевода однородных координат в декартовы координаты производится автоматически.
Матрица (1) является шаблоном для матрицы перспективой проекции. Как было сказано ранее, задача матрицы проекции заключается в двух моментах: установка пользовательской системы координат (левосторонняя или правосторонняя), перенос объёма видимости наблюдателя в CVV. Выведем перспективную матрицу для левосторонней пользовательской системы координат.
Матрицу проекции можно описать с помощью четырёх параметров (рис. 3):
- Угол обзора в радианах (fovy );
- Соотношение сторон (aspect );
- Расстояние до ближней плоскости отсечения (n );
- Расстояние до дальней плоскости отсечения (f ).
Рис. 3. Перспективный объём видимости
Рассмотрим проекцию точки в пространстве наблюдателя на переднюю грань отсечения перспективного объёма видимости. Для большей наглядности на рис. 4 изображён вид сбоку. Так же следует учесть, что пользовательская система координат совпадает с системой координат CVV, то есть везде пользуется левосторонняя система координат.
Рис. 4. Проецирование произвольной точки
На основании свойств подобных треугольников справедливы следующие равенства:
Выразим yꞌ и xꞌ:
В принципе, выражений (2) достаточно для получения координат точек проекции. Однако для правильного экранирования трёхмерных объёктов необходимо знать глубину каждого фрагмента. Другими словами необходимо хранить значение компоненты z . Как раз это значение используется при тестах глубины OpenGL. На рис. 3 видно, что значение zꞌ не подходит в качестве глубины фрагмента, потому что все проекции точек умеют одинаковое значение zꞌ . Выход из сложившейся ситуации – использование так называемой псевдоглубины.
Свойства псевдоглубины:
- Псевдоглубина рассчитывается на основании значения z ;
- Чем ближе к наблюдателю находится точка, тем меньшеe значение имеет псевдоглубина;
- У всех точек, лежащих на передней плоскости объёма видимости, значение псевдоглубины равно -1;
- У всех точек, лежащих на дальней плоскости отсечения объёма видимости, значение псевдоглубины равно 1;
- Все фрагменты, лежащие внутри объёма видимости, имеют значение псевдоглубины в диапазоне [-1 1].
Коэффициенты a и b необходимо вычислить. Для того чтобы это сделать, воспользуемся свойствами псевдоглубины 3 и 4. Получаем систему из двух уравнений с двумя неизвестными:
Произведём сложение обоих частей системы и умножим результат на произведение fn , при этом f и n не могут равняться нулю. Получаем:
Раскроем скобки и перегруппируем слагаемые так, чтобы слева осталась только часть с а , а справа только с b :
Подставим (6) в (5). Преобразуем выражение к простой дроби:
Умножим обе стороны на -2fn , при этом f и n не могут равняться нулю. Приведём подобные, перегруппируем слагаемые и выразим b :
Подставим (7) в (6) и выразим a :
Соответственно компоненты a и b равны:
Теперь подставим полученные коэффициенты в матрицу заготовку (1) и проследим, что будет происходить с координатой z для произвольной точки в однородном пространстве наблюдателя. Подстановка выполняется следующим образом:
Пусть расстояние до передней плоскости отсечения n
равно 2, а расстояние до дальней плоскости отсечения f
равно 10. Рассмотрим пять точек в однородном пространстве наблюдателя:
| Точка | Значение |
Описание |
|---|---|---|
| 1 | 1 | Точка находится перед передней плоскостью отсечения объёма видимости. Не проходит растеризацию. |
| 2 | 2 | Точка находится на передней грани отсечения объёма видимости. Проходит растеризацию. |
| 3 | 5 | Точка находится между передней гранью отсечения и дальней гранью отсечения объёма видимости. Проходит растеризацию. |
| 4 | 10 | Точка находится на дальней грани отсечения объёма видимости. Проходит растеризацию. |
| 5 | 20 | Точка находится за дальней гранью отсечения объёма видимости. Не проходит растеризацию. |
Умножим все точки на матрицу (8), а затем переведём полученные однородные координаты в декартовые координаты . Для этого нам необходимо вычислить значения новых однородных компонент
и
.
Точка 1:
Обратите внимание, что однородная координата абсолютно верно позиционируется в CVV, а самое главное, что теперь возможна работа теста глубины OpenGL, потому что псевдоглубина полностью удовлетворяет требованиям тестов.
С координатой z разобрались, перейдём к координатам x и y . Как говорилось ранее весь перспективный объём видимости должен умещаться в CVV. Длина ребра CVV равна двум. Соответственно, высоту и ширину перспективного объёма видимости надо сжать до двух условных единиц.
В нашем распоряжении имеется угол fovy и величина aspect . Давайте выразим высоту и ширину, используя эти величины.
Рис. 5. Объём видимости
Из рис. 5 видно, что:
Теперь можно получить окончательный вид перспективной проекционной матрицы для пользовательской левосторонней системы координат, работающей с CVV OpenGL:
На этом вывод матриц закончен.
Пару слов о DirectX - основном конкуренте OpenGL. DirectX отличается от OpenGL только габаритами CVV и его позиционированием. В DirectX CVV - это прямоугольный параллелепипед с длинами по осям x и y равными двойке, а по оси z длина равна единице. Диапазон x и y равен [-1 1], а диапазон z равен . Что касается системы координат CVV, то в DirectX, как и в OpenGL, используется левосторонняя система координат.
Для вывода перспективных матриц для пользовательской правосторонней системы координат необходимо перерисовать рис. 2, рис.3 и рис.4 с учётом нового направления оси Z . Далее расчёты полностью аналогичны, с точностью до знака. Для матриц DirectX свойства псевдоглубины 3 и 4 модифицируются под диапазон .
На этом тему перспективных матриц можно считать закрытой.
Аксонометрия является параллельной проекцией. В табл.3.3 первыми приводятся матрицы ортографических проекций на координатные плоскости, полученные из их определений.
Табл.3.3.Матрицы проектирующих преобразований и проецирования
|
Ортографическая проекция на XOY |
Ортографическая проекция на YOZ |
|
|
|
||
|
Ортографическая проекция на XOZ |
Ортографическая проекция на плоскость x=p |
|
|
|
|
|
|
Матрица триметрического преобразования на плоскость XOY |
||
|
|
||
|
Матрица изометрического преобразования на плоскость XOY |
||
|
|
||
|
Матрица изометрического проецирования на плоскость XOY |
||
|
|
||
|
Матрица косоугольной проекции на XOY |
Матрица свободной проекции на XOY |
|
|
|
|
|
|
Матрица кабинетной проекции на XOY |
Матрица перспективного преобразования с одной точкой схода (картинная плоскость перпендикулярна оси абсцисс) |
|
|
|
|
|
|
Матрица перспективного преобразования с одной точкой схода (картинная плоскость перпендикулярна оси ординат) |
Матрица перспективного преобразования с одной точкой схода (картинная плоскость перпендикулярна оси аппликат) |
|
|
|
|
|
|
Матрица перспективного преобразования с двумя точками схода (картинная плоскость параллельна оси ординат) |
Матрица перспективного преобразования с тремя точками схода (картинная плоскость произвольного положения) |
|
|
|
|
|
Изометрия,
диметрия и триметрия получаются
комбинацией поворотов, за которыми
следует проекция из бесконечности. Если
нужно описать проекцию на плоскость
XOY, то сначала необходимо осуществить
преобразование поворота на угол
 относительно оси ординат, затем на угол
относительно оси ординат, затем на угол относительно оси абсцисс. В табл.3.3
приведена матрица триметрического
преобразования. Для получения матрицы
диметрического преобразования, при
котором, например, коэффициенты искажения
по осям абсцисс и ординат будут равными,
взаимосвязь между углами поворотов
должна подчиняться зависимости
относительно оси абсцисс. В табл.3.3
приведена матрица триметрического
преобразования. Для получения матрицы
диметрического преобразования, при
котором, например, коэффициенты искажения
по осям абсцисс и ординат будут равными,
взаимосвязь между углами поворотов
должна подчиняться зависимости
То
есть, выбрав угол
 ,
можно вычислить угол
,
можно вычислить угол и определить матрицу диметрической
проекции. Для изометрического
преобразования взаимосвязь этих углов
превращается в строго определенные
значения, составляющие:
и определить матрицу диметрической
проекции. Для изометрического
преобразования взаимосвязь этих углов
превращается в строго определенные
значения, составляющие:
В табл.3.3 приведена матрица изометрического преобразования, а также матрица изометрического проецирования на плоскость XOY. Необходимость в матрицах первого типа заключается в их использовании в алгоритмах удаления невидимых элементов.
В косоугольных проекциях проектирующие прямые образуют с плоскостью проекции угол, отличный от 90 градусов. В табл.3.3 приведена общая матрица косоугольной проекции на плоскость XOY, а также матрицы свободной и кабинетной проекций, в которых:
Перспективные проекции (табл.3.3) также представлены перспективными преобразованиями и перспективными проекциями на плоскость XOY. V X , V Y и V Z являются центрами проецирования - точками на соответствующих осях. –V X , -V Y , -V Z будут точками, в которых сходятся пучки прямых, параллельных соответствующим осям.
Система координат наблюдателя представляет собой левую систему координат (рис.3.3), в которой ось z e направлена из точки зрения вперед, ось x e направлена вправо, а ось y e – вверх. Такое правило принято для совпадения осей x e и y e с осями x s и y s на экране. Определение значений координат экрана x s и y s для точки Р приводит к необходимости деления на координату z e . Для построения точного перспективного образа необходимо выполнять деление на координату глубины каждой точки.
В табл.3.4 приведены значения дескриптора вершин S(X,Y,Z) модели (рис.2.1), подвергнутой преобразованиям поворотов и изометрическому преобразованию.
Табл.3.4.Дескрипторы вершин модели
|
Исходная модель |
M(R(z,90))xM(R(y,90)) |
|
|||||||
Для детального описания методов отслеживания точечных особенностей, калибровки камеры и реконструкции трехмерных объектов необходимо ввести модель перспективной проектирования и описать геометрические свойства этого преобразования. Точки нескольких изображений, полученных с помощью перспективной проекции, находятся в особых отношениях друг с другом, которые описываются эпиполярной геометрией. Модели этих отношений должны быть подробно рассмотрены, т.к. практически все методы трехмерной реконструкции требуют оценки соответствующих моделей и опираются на их свойства.
Необходимо отметить отдельно предположение, что на всех исходных изображениях запечатлена одна и та же сцена, т.е. каждое изображение является видом сцены с какой-то определенной камеры. Поэтому для удобства описания вводится понятие вида, как изображение с ассоциированной с ним моделью камеры, с которой оно было получено.
Перспективная проекция
Модель перспективной проекции соответствует идеальной камере-обскуре. Эта модель довольно точно соответствует процессу построения изображения в большинстве современных фото- и видеокамер. Однако из-за ограничений современной оптики реальный процесс несколько отличается от модели камеры-обскуры. Отличия реального процесса от модели называются искажениями и моделируются отдельно.
Модель простейшей камеры-обскуры удобна тем, что она полностью описывается центром проекции и положением плоскости изображения. Поэтому проекция любой точки сцены на изображении может быть найдена как пересечение луча, соединяющего центр проекции и точку сцены, с плоскостью изображения.
Простейшая модель перспективной проекции
Рассмотрим простейший случай, когда центр проекции камеры (фокус) помещен в начало системы координат, и плоскость изображения совпадает с плоскостью Z=1. Пусть (X,Y,Z) - координаты точки в 3-х мерном пространстве, а (x,y) - проекция этой точки на изображение I. Перспективная проекция в этом случае описывается следующими уравнениями:
В матричной форме с использованием однородных координат эти уравнения переписываются в следующем виде:
 (2.2)
(2.2)
Плоскость, расположенная на расстоянии 1 от центра проекции, и перпендикулярная оптической оси называется идеальной плоскостью изображения. Оптическая ось пересекает идеальную плоскость изображения в точке с, называемой принципиальной точкой. Иллюстрация простейшего случая перспективной проекции приведена на рис. 1.
Внутренняя калибровка камеры
Простейший случай перспективной проекции практически всегда не соответствует реальной камере. Расстояние от центра проекции до плоскости изображения, т.е. фокусное расстояние, обозначаемое f, обычно не равно 1. Также координаты точки в плоскости изображения могут не совпадать с абсолютными координатами. При использовании цифровой камеры, соотношение между координатами точки в изображении и абсолютными координатами точки на идеальной плоскости, определяется формой и размерами пикселов матрицы.

Обозначим размеры пиксела матрицы цифровой камеры за p x , p y , угол наклона пиксела за α, а принципиальную точку за , рис.2. Тогда координаты точки (x,y) в изображении, соответствующей точке (x R , y R) на идеальной плоскости, определяются выражением:
 (2.3)
(2.3)
Если за f x ,f y обозначить фокусное расстояние f, измеренное в ширинах и высотах пикселей, а tan(α)*f/p y обозначить как s, то формула 2.3 преобразуется в:
 (2.4)
(2.4)
Матрица K называется матрицей внутренней калибровки камеры. В большинстве случаев у реальных цифровых камер угол наклона пикселей близок к прямому, т.е. параметр s=0, а ширина и высота пикселя равны. Принципиальная точка обычно располагается в центре изображения. Поэтому матрица K может быть записана в виде:
 (2.5)
(2.5)
Это предположение о виде матрицы K широко используются для упрощения алгоритмов определения внутренней калибровки камеры, а также при синтетическом моделировании изображений, необходимых для оценки качества и эффективности методов трехмерной реконструкции.

Внешняя калибровка камеры
Пусть M - точка сцены в 3-х мерном пространстве. Любое движение является евклидовым преобразованием пространства, поэтому в однородных координатах оно выражается как:
 (2.6)
(2.6)
где R - матрица вращения, T= T - вектор переноса.
Движение камеры относительно сцены эквивалентно обратному движению точек сцены относительно камеры, поэтому равно:
 (2.7)
(2.7)
где R, T - матрица вращения и вектор перемещения камеры относительно сцены. Матрица С называется матрицей внешней калибровки камеры. Матрица C -1 называется матрицей движения камеры . Таким образом, матрица внешней калибровки камеры переводит координаты точек сцены из системы координат сцены в систему координат, связанную с камерой.
Полная модель перспективной проекции
Из выражений 2.1, 2.4, 2.7 можно вывести выражение произвольной перспективной проекции для любой камеры с произвольной ориентацией и положением в пространстве:

В более краткой форме с учетом предыдущих обозначений эта формула может быть записана как:

Матрица P называется матрицей проекции камеры.
По аналогии с общим перспективным преобразованием рассмотрим вначале простейший случай перспективного преобразования плоскости. Пусть плоскость p совпадает с плоскостью Z=0, тогда однородные трехмерные координаты любой ее точки M=. Для любой камеры с матрицей проекции P, перспективное преобразование плоскости описывается матрицей размерности 3*3:


Поскольку любую плоскость в 3-х мерном пространстве можно перевести в плоскость Z = 0 евклидовым преобразованием поворота и переноса, что эквивалентно домножению матрицы камеры P на матрицу преобразования L, то перспективное отображение произвольной плоскости в пространстве описывается линейным преобразованием с матрицей размерности 3*3.
Перспективное преобразование плоскости также называется гомографией . В матричной форме перспективное преобразование плоскости записывается как m=HM .

Геометрия двух изображений
Запечатленная на всех исходных изображениях сцена считается неподвижной, поэтому взаимное расположение проекций точек сцены на разных кадрах не может меняться произвольным образом. Ограничения, накладываемые на расположение проекций точек, очевидно зависят от параметров камер и их положения друг относительно друга. Поэтому определение моделей таких ограничений дает часть информации о взаимном расположении камер, с которых были получены изображения.
Перспективное преобразование плоскости
Если центры двух камер совпадают, то точки на плоскостях изображения обеих камер переводятся друг в друга перспективным преобразованием плоскости. В этом случае, преобразование точек между изображениями не зависит от формы 3-х мерной сцены, а зависит только от взаимного положения плоскостей изображений.

Если вся сцена или ее часть представляет собой плоскость, то ее изображения на разных видах с несовпадающими центрами камер, можно перевести друг в друга преобразованием гомографии. Пусть p - наблюдаемая плоскость, H 1 - преобразование гомографии между плоскостью p и изображением I 1 , H 2 - преобразование гомографии между плоскостью p и изображением I 2 . Тогда преобразование гомографии H 12 между изображениями I 1 и I 2 можно вывести следующим образом:

H 12 не зависит от параметризации плоскости p, а значит не зависит и от системы координаты в пространстве
Большинство методов определения координат 3х мерных точек по их проекциям и методов реконструкции 3-х мерной сцены, опираются на предположение о движении центра камеры между видами. Поэтому при совпадении центров камер нескольких видов эти методы будут давать некорректные результаты. Такие конфигурации камер должны обнаруживаться и обрабатываться специальным образом.

Поскольку преобразование гомографии записано в однородных координатах, то матрица H определена с точностью до масштаба. Она имеет 8 степеней свободы, и параметризируется 8 переменными. Каждое известная пара соответствующих точек m 1 и m 2 на первом и втором изображении соответственно дает 2 линейных уравнения от элементов матрицы H. Поэтому 4-х известных пар соответствующих точек достаточно для составления системы линейных уравнений из 8 уравнений с 8 неизвестными. По этой системе гомография H может быть однозначно определена, если никакие три из точек не лежат на одной прямой.
Фундаментальная матрица
Рассмотрим случай, когда центры камер двух видов не совпадают. Пусть C 1 и C 2 - центры двух камер, M - 3-х мерная точка сцены, m 1 и m 2 - проекции точки M на первое и второе изображение соответственно. Пусть П - плоскость, проходящая через точку M и центры камер C 1 и C 2 . Плоскость П пересекает плоскости изображений первого и второго видан по прямым l 1 и l 2 . Поскольку лучи C 1 M и C 2 M лежат в плоскости П, то очевидно, что точки m 1 и m 2 лежат на прямых l 1 и l 2 соответственно. Можно дать более общее утверждение, что проекции любой точки M", лежащей в плоскости П, на оба изображения должны лежать на прямых l 1 и l 2 . Эти прямые называются эпиполярными линиями. Плоскость П называются эпиполярной плоскостью.

Два вида одной и той же сцены называются стереопарой, а отрезок C 1 C 2 , соединяющий центры камер, называется базой стереопары (baseline) или стереобазой. Любая эпиполярная плоскость проходит через отрезок C 1 C 2 . Пусть C 1 C 2 пересекает первое и второе изображение в точках e 1 и e 2 соответственно. Точки e 1 и e 2 называются эпиполярными точками или эпиполями. Все эпиполярные линии пересекаются в точках e 1 и e 2 на первом и втором изображении соответственно. Множество эпиполярных плоскостей представляет собой пучок, пересекающийся по стереобазе C 1 C 2 . Множество эпиполярных линий на обоих изображений также представляют собой пучки прямых, пересекающихся в e 1 и e 2 .
Точки m 1 и m 2 называются соответствующими, если они являются проекциями одной и той же точки сцены M. Эпиполярные линии l 1 и l 2 называются соответствующими, если они лежат в одной и той же эпиполярной плоскости П. Если эпиполярная плоскость П проходит через точку m 1 , тогда эпиполярные линии l 1 и l 2 , лежащие в ней, называются соответствующими точке m 1 .

Ограничение на положение соответствующих точек m 1 и m 2 , вытекающей из эпиполярной геометрии, можно сформулировать следующим образом: точка m 2 , соответствующая m 1 , должна лежать на эпиполярной линии l 2 , соответствующей m 1 . Это условие называется эпиполярным ограничением. В однородных координатах условие того, что точка m лежит на линии l записывается как l T m=0 . Эпиполярная линия проходит также через эпиполярную точку. Уравнение прямой, проходящей через точки m 1 и e 1 можно записать как:
l 1 ∼ x m 1 ,
где x - антисимметричная матрица размерности 3*3 такая что, x m 1 - векторное произведение m 1 и e 1 .
Для соответствующих эпиполярные линий l 1 и l 2 верно:

где P + - псевдоинверсия матрицы P.
Матрица F называется фундаментальной матрицей. Она представляет собой линейный оператор, сопоставляющей каждой точке m 1 соответствующую ей эпиполярную линию l 2 . Для каждой пары соответствующих точек m 1 и m 2 верно
m T 2 Fm 1 =0
Это формулировка эпиполярного ограничения через фундаментальную матрицу.
Фундаментальная матрица имеет 7 степеней свободы. Каждая пара соответствующих точек m 1 и m 2 задает одно линейное уравнение на элементы матрицы, поэтому она может быть вычислена по известным 7 парам соответствующих точек.
Эпиполярное ограничение справедливо для любых пар соответствующих точек, расположенных на идеальных плоскостях двух видов. Если известны матрицы внутренней калибровки K 1 и K 2 камер обоих видов, то эпиполярное ограничение для соответствующих точек на идеальных плоскостях записывается как:

Матрица E называется существенной матрицей. Можно показать, что существенная матрица также может быть получена из взаимного расположения камер.
Пусть P 1 =(I|0) и P 2 =(R|-RT) - две матрицы проектирования с калибровкой K = I. Тогда уравнения проектирования на идеальную плоскость обеих камер записываются в виде:

Найдем эпиполярную линию на втором виде, соответствующую точке m" 1 на первом. Для этого достаточно спроектировать на второй вид две точки, лежащие на луче (C 1 ,m" 1) на второй вид, например центр первой камеры (0,0,0,1) T и точку на плоскости бесконечности (x" 1 ,y" 1 ,z" 1 ,0) T . Проекциями этих точек будут являться соответственно -RT, и R(x" 1 ,y" 1 ,z" 1 ,0) T . Уравнение эпиполярной линии l 2 , проходящей через обе этих точки задается как векторное произведение:
l 2 =RT×R(x" 1 ,y" 1 ,z" 1) T =R(T×(x" 1 ,y" 1 ,z" 1) T)
В матричной форме векторне произведение T×(x" 1 ,y" 1 ,z" 1) T можно записать с помощью матрицы S:

Тогда эпиполярное ограничение на точки в идеальной плоскости записывается как:

Выражение существенной матрицы через параметры внешней калибровки двух камер используется для вычисления относительного положения камер.

Геометрические свойства трех и более изображений
Пусть C 1 ,C 2 и C 3 - центры трех видов одной и той же трехмерной сцены. В этом случае, эпиполярные ограничения накладываются на соответствующие точки любой пары видов. Если известны проекции двух точек m 1 и m 2 на первый и второй вид, то положение проекции на третье изображение может быть найдено как пересечение двух эпиполярных видов, соответствующих точкам m 1 и m 2 .
По двум известным проекциям m 1 и m 2 на два изображения с известной калибровкой можно определить положение точки M в пространстве. Поэтому если известна калибровка третьего изображения, то проекция точки M на третий вид может быть определена простой проекцией.
Ограничения, накладываемые на положение соответствующих точек более двух изображений, также можно записать в линейной форме. Для трех видов эти ограничения записываются в виде трифокального тензора, для четырех видов - в форме квадрифокального тензора. Однако вычисление этих ограничений эквивалентно вычислению калибровки всех трех или четырех видов в проективном пространстве. В этой работе эти виды ограничений не используются, поэтому более подробно не рассматриваются.